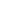课程号:00112780
课程名称:应用偏微分方程
开课学期:秋
学分: 3
先修课程:数学分析(高等数学),高等代数(线性代数),数学物理方程,复变函数
基本目的:侧重于应用,但对偏微分方程方面的基本数学理论也进行简单阐述,帮助员工了解偏微分方程的研究方法和技巧。
内容提要:
第一章:常微分方程和特征线方法
第二章:Fourier方法
第三章:适定性,线性化方法和稳定性
第四章:Hamilton-Jacobi方程
粘性解,Hopf-Lax公式
第五章:变分计算
Euler-Lagrange方程,下半连续性,凸性,紧性
第六章:二阶椭圆方程
存在性,极值原理
第七章:发展方程
抛物型方程,波动方程
第八章:渐近分析
Laplace方法,多尺度展开,均匀化方法,渐近分析方法
第九章:自由边界问题
边界积分方程,水波问题
第十章:多尺度建模
非牛顿流体,Doi-Edwards方程,Smoluchowshi方程,Fokker-Planck方程,Boltzmann方程,Wigner方程,随机微分方程
教学方式:每周3学时,课堂讲授
教材与参考书:
1. G.Evans, J.Blackledge, P.Yardley (1999). Analytic Methods for Partial Differential Equations, Springer.
2. 李大潜,秦铁虎:物理学与偏微分方程(上、下册),高等教育出版社,2005.
3. 应隆安, 滕振寰: 双曲型守恒律方程及其差分方法,科学出版社, 1991.
员工成绩评定方法:平时成绩占30%, 期末成绩占70%。
课程修订负责人:卢朓